ИПМ ДВО РАН

Наиболее важные научные результаты ИПМ ДВО РАН

2024г.

1. По данным ГНСС-наблюдений получены характеристики ионосферных возмущений (особенности распространения, амплитудно-частотные характеристики, рисунок 1) над Приморским краем и смежными регионами, инициированных мощнейшим взрывным извержением вулкана Хунга-Тонга-Хунга-Хаапай 15 января 2022 г., архипелаг Тонга. Полученные по ГНСС-наблюдениям результаты сопоставлены с данными комплекса лазерного деформографа и нанобарографа, установленных на МЭС «Мыс Шульца». Обнаружены временные задержки между моментами фиксации возмущений в тропосфере и ионосфере порядка 50 мин, происхождение которых на данный момент до конца не выяснено (рисунок 2).

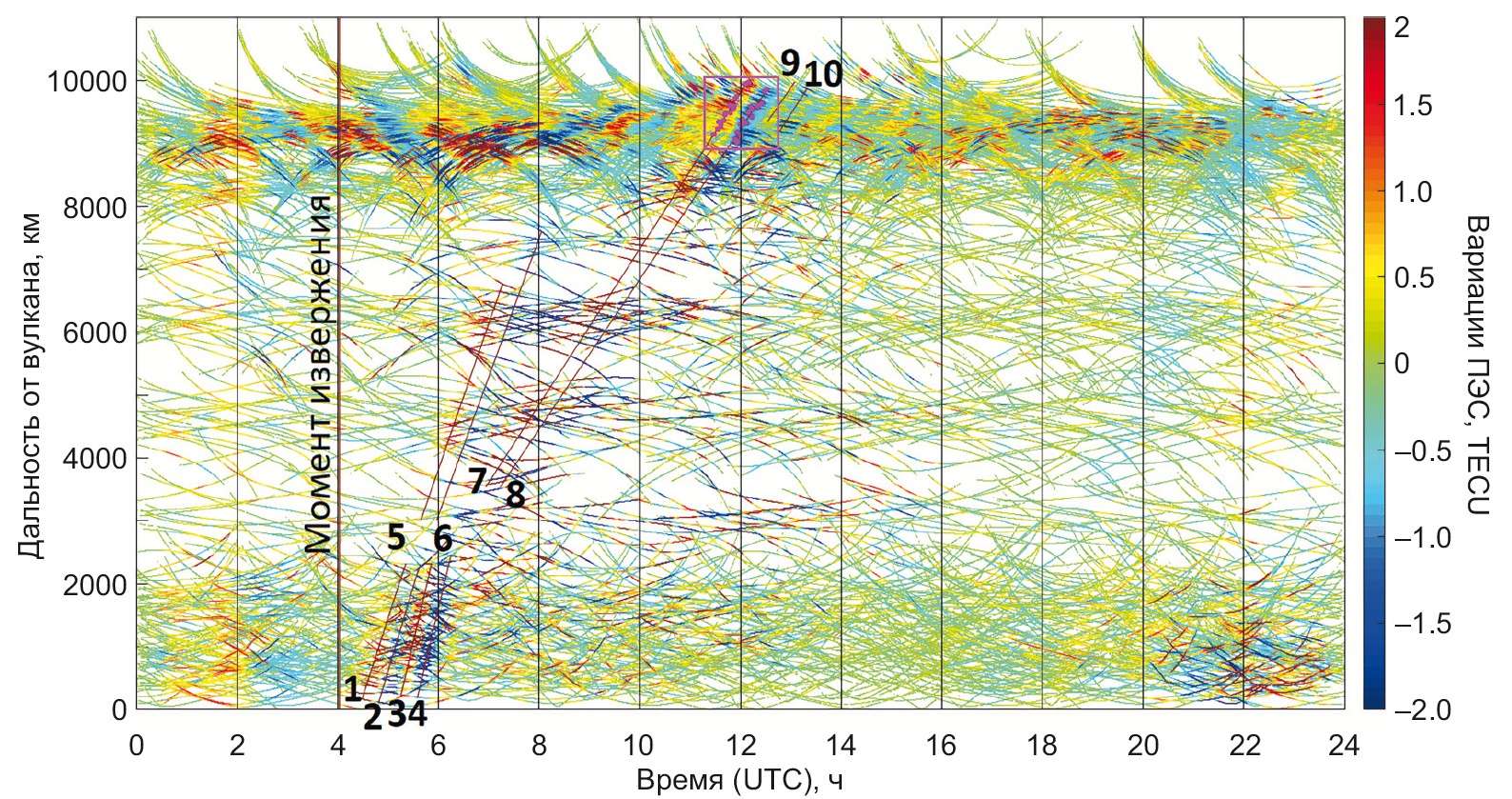
Рисунок 1 – Диаграмма дальность – время за 15.01.2022 г., построенная для периода фильтрации сигнала 10–60 мин. Прямыми линиями и цифрами обозначены фронты зарегистрированных ионосферных возмущений, ассоциируемые с извержением вулкана. Красным квадратом показана область возмущений, обнаруженных над Приморским краем.

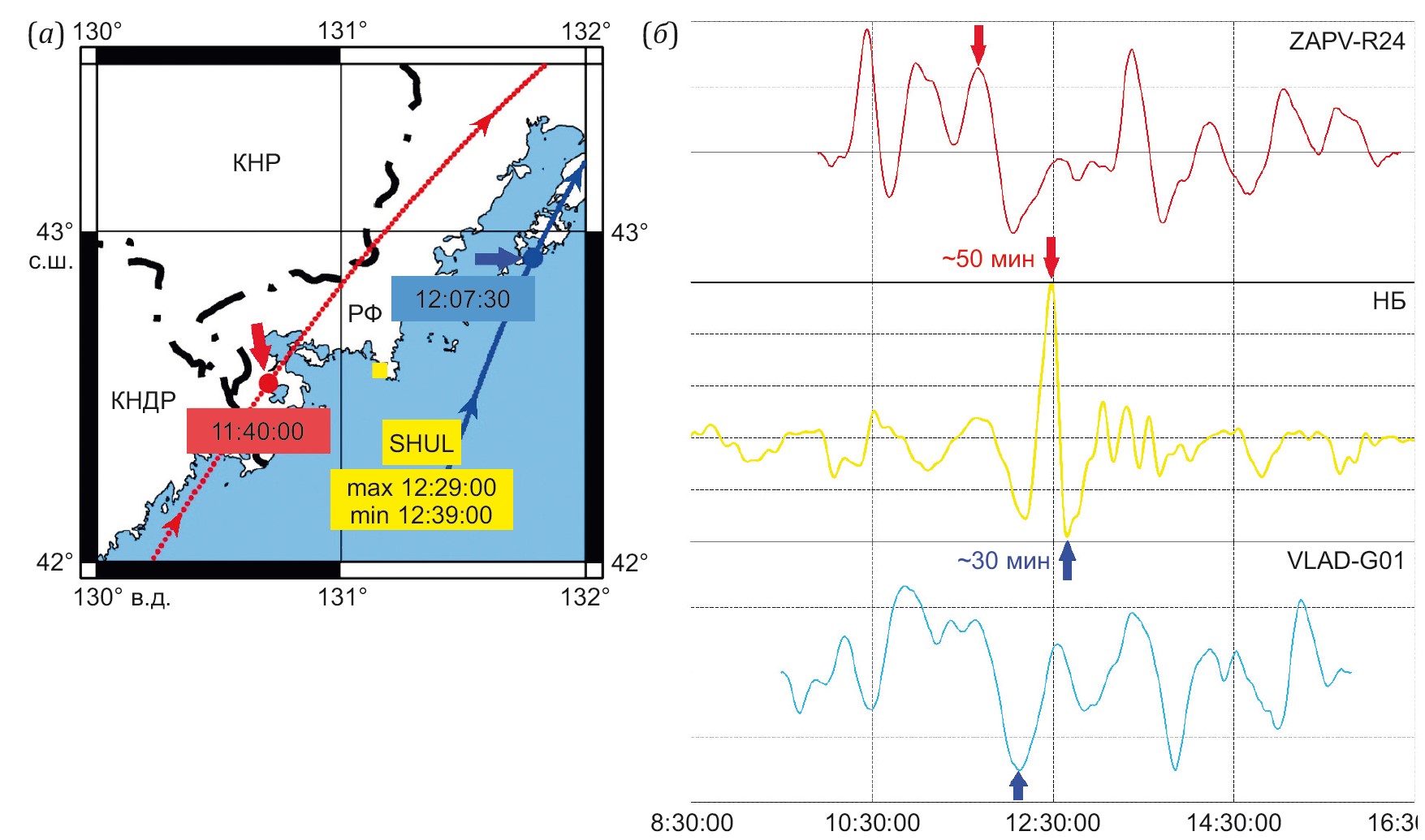
Рисунок 2 – Положение моментов фиксации пиков возмущений (а) и сравнение моментов фиксации по ГНСС-данным и данным нанобарографа (б). (а) – красная линия – траектория движения спутника для пары станция «ZAPV» – спутник R24 (ГЛОНАСС); синяя линия – траектория движения спутника для пары станция «VLAD» – спутник G01 (GPS); красным цветом показана точка и время фиксации максимума по ГНСС-данным, синим – минимума по ГНСС-данным, желтым – положение НБ (SHUL), а также время фиксации максимума и минимума по данным НБ. (б) – красными стрелками показаны максимумы возмущений по ГНСС-данным и данным НБ, синими стрелками – минимумы возмущений по ГНСС-данным и данным НБ; красным и синим цветом даны разности моментов фиксации максимумов и минимумов соответственно.

М.А. Болсуновский, Н.В. Шестаков, Г.И. Долгих, Н.П. Перевалова, А.С. Тен. Ионосферные возмущения над Приморским краем, вызванные извержением вулкана Хунга-Тонга-Хунга-Хаапай 15 января 2022 г. // Геодинамика и тектонофизика. 2024. Т. 15. № 1. Номер публикации 0738. С. 1-16. DOI: 10.5800/GT-2024-15-1-0738.

2. Разработаны корректные математические модели и эффективные, устойчивые численные алгоритмы, реализованные с использованием метода гибридных конечных элементов на параллельных компьютерных платформах, для моделирования непрерывных пространственно-временных многомасштабных определяющих параметров тепломассопереноса с определением остаточных технологических напряжений в лазерных аддитивных технологиях металлоизделий. Предложен новый способ исследования динамических процессов путем наращивания лежащей капли (рисунок 3). Показано существенное влияние потока газа и массового расхода порошка на структуру конвекции расплава с образованием дополнительного вихря (рисунок 4) и кратера на вершине растущей капли. Исследовано влияние технологических режимов и механизмов упрочнения и разупрочнения в наращиваемом слое металла на эволюцию технологических напряжений. Данный подход интегрируется в интеллектуальные информационные системы управления 3D-печати и позволяет значительно сократить период разработки лазерной технологии выращивания металлоизделий. Разработанные математические модели и методики расчета могут быть использованы для совершенствования существующих и разработки новых технологий 3D-печати металлоизделий, защитных покрытий и создание принципиально новых материалов.

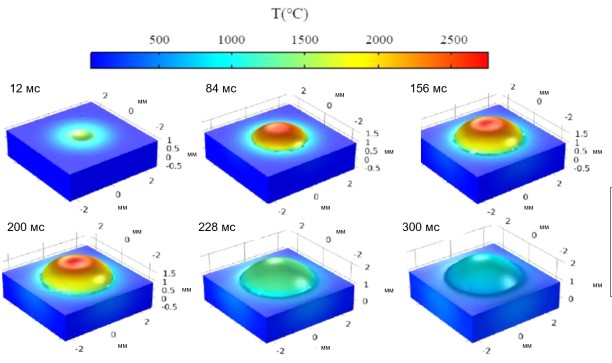
Рисунок 3 - Эволюция геометрии и температуры растущей капли при лазерном наращивании (трехмерная модель)

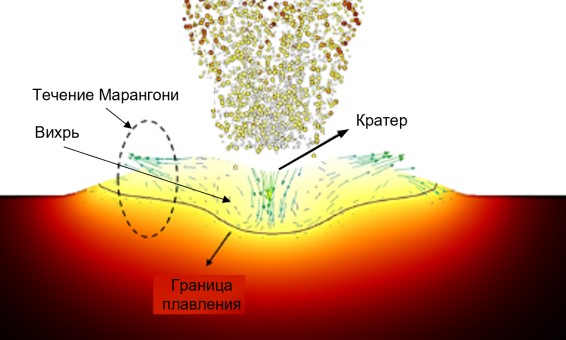
Рисунок 4 - Структура течения в окрестности кратера на вершине растущей капли расплава

Chekhonin K.A. Current state and development of the theory of curing high-energy composite polymer materials // Журнал Сибирского федерального университета. Математика и физика. 2024. – Т. 17. – N 1. – С. 106-114.

Гриценко А.А., Чехонин К.А. Численное моделирование остаточных напряжений в формируемом металлическом слое с использованием подвижного лазерного источника энергии // Дальневосточный математический журнал. 2024. – Т. 23. – № 1. – С. 22–32.

Белозеров Н.И., Чехонин К.А. Трехмерное конечно-элементное моделирование течения расплава металла со свободной поверхностью в условиях движущегося лазерного источника // Дальневосточный математический журнал. 2024. – Т. 23. – № 1. – С. 9–21.

3. Исследован широкий класс новых краевых задач для усложненных моделей тепломассопереноса, рассматриваемых при неоднородных краевых условиях для скорости и диффузионной компоненты. Рассматривается тот важный для приложений случай, когда теплофизические параметры зависят от температуры в случае теплопроводящей жидкости либо от концентрации растворенного вещества в случае бинарной жидкости, а основные компоненты решения удовлетворяют неоднородным краевым условиям. Разработан математический аппарат исследования указанных краевых задач, моделирующих течения реальных жидкостей в различного рода двумерных и трехмерных каналах, примеры которых приведены на рисунке 5. На основе разработанного аппарата установлены важные свойства решений (включая глобальную разрешимость, локальную единственность и принцип максимума для концентрации).

Проведенное исследование имеет высокий потенциал в задачах химической технологии, металлургии при разработке эффективных технологий бесконтактного размешивания расплавленных металлов и в ядерной индустрии при создании эффективных систем жидкометаллического охлаждения устройств ядерной энергетики.

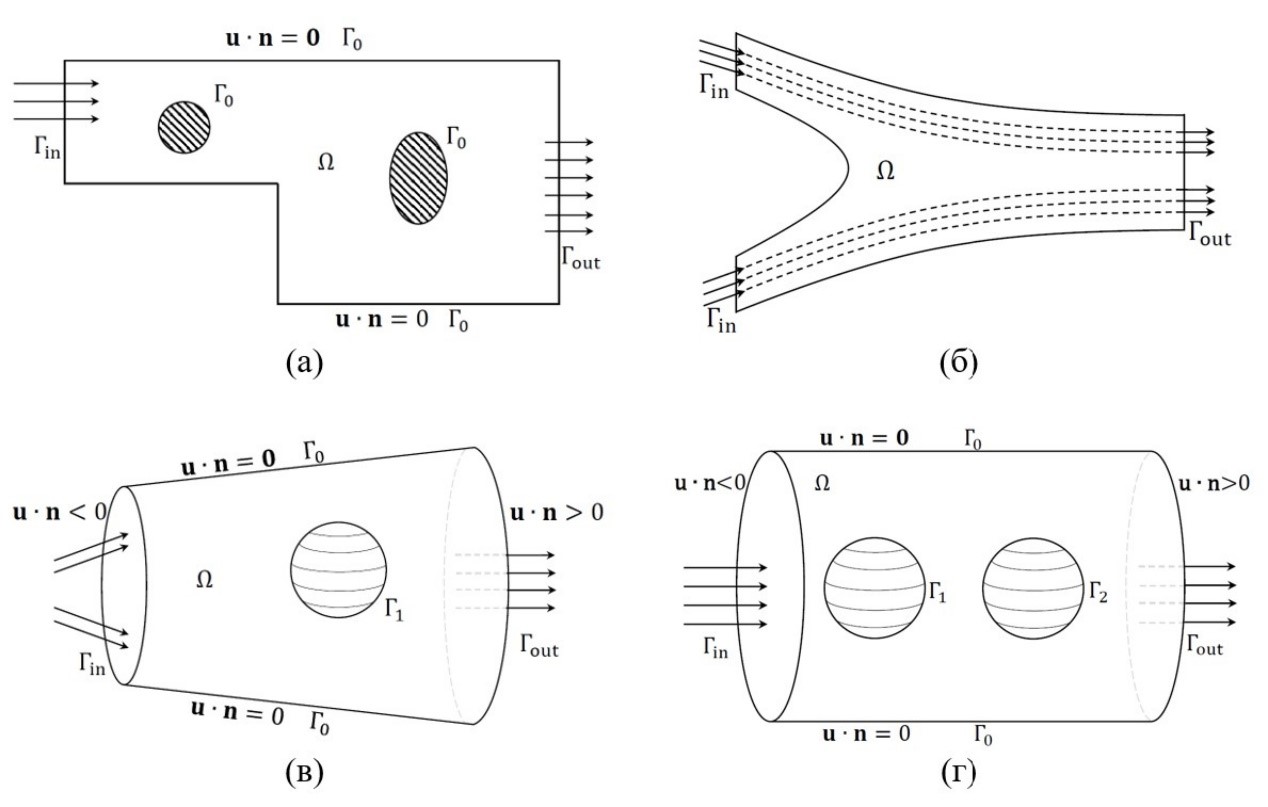
Рисунок 5 – Типичные примеры гидродинамических каналов с возможными препятствиями внутри канала при неоднородных граничных условиях для скорости и диффузионной компоненты на входе Γ_in и выходе Γ_out: (а) плоский ступенчатый канал с двумя препятствиями Γ_0; (б) плоский канал с двумя входами и одним выходом; (в) трехмерный канал; (г) цилиндрический канал с двумя препятствиями Γ_1 и Γ_2

Alekseev G.V., Soboleva O.V. Inhomogeneous boundary value problems for the generalized Boussinesq model of mass transfer // Mathematics. 2024. V. 12, Is. 3. N 391. DOI: 10.3390/math12030391. (Q1, IF=2.2, 1 уровень)

Alekseev G.V., Soboleva O.V. Solvability analysis for the Boussinesq model of heat transfer under the nonlinear Robin boundary condition for the temperature // Philosophical Transactions of the Royal Society A. 2024. V. 382. N 20230301. DOI: 10.1098/rsta.2023.0301. (Q1, IF=4.3, 1 уровень)

Алексеев Г.В., Спивак Ю.Э. Анализ смешанной краевой задачи для стационарной модели конвекции вещества с переменными ведущими коэффициентами // Прикладная механика и техническая физика. 2024. T. 65, N 5. DOI: 10.15372/PMTF202415509. (Q3, IF=0.6, 2 уровень)

4. Произведен численный расчет фазовой диаграммы плоской решетки спинов в модели Эдвардса-Андерсена (частный случай модели Изинга с переменными обменными интегралами) без воздействия внешнего поля и в поле. Фазовая диаграмма рассчитана с помощью авторской реализации параллельного алгоритма исчерпывающего перечисления. Необходимо отметить, что для модели Эдвардса-Андерсона в настоящее время не существует строгого решения с помощью аналитических методов.

Проведён строгий расчет параметров статистической суммы (вырождение, энергия, спиновый избыток). Показано, что линия Альмейды-Таулесса (рисунок 6) не является следствием неэргодичности материалов спинового стекла. Полученные результаты численных расчетов потенциально могут быть при использованы в разработке новой электроники, для создания вычислителей, систем магнитной памяти и в индустрии наносистем и наноматериалов.

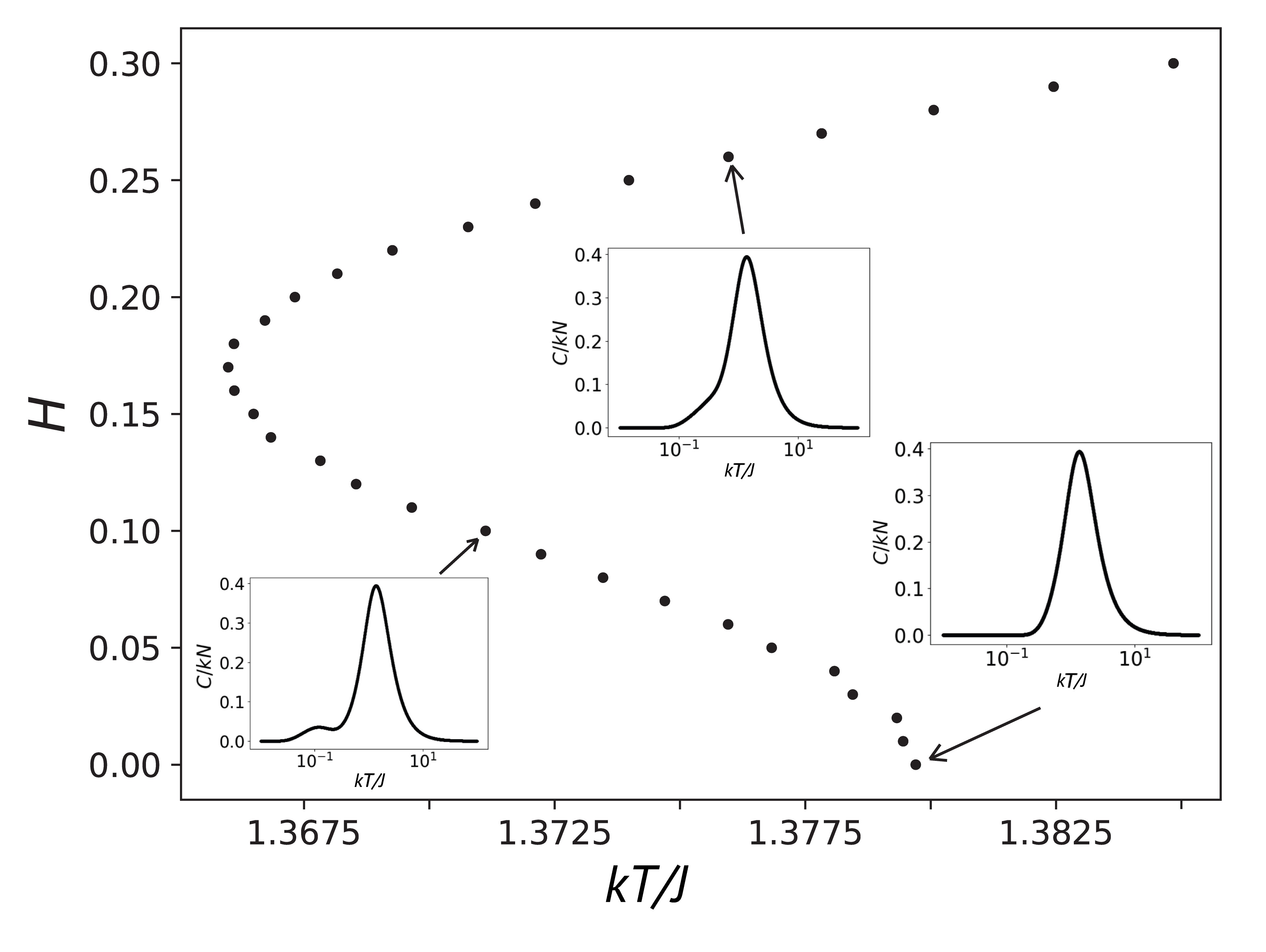
Рисунок 6 – Линия нестабильности конечной системы Эдвардса-Андерсена. Во внешнем магнитном поле. На вставках показано температурное поведение теплоемкости во внешнем магнитном поле для системы P+ = 0.5

V.O. Trukhin, V.S. Strongin, M.A. Chesnokov, A.G. Makarov, E.A. Lobanova, Y.A. Shevchenko, K.V. Nefedev. Thermodynamic equilibrium of ±J Ising model on square lattice // Physica A: Statistical Mechanics and its Applications. 2024. Volume 655. ISSN 0378-4371 (Q2, IF=2.8)

5. На основе проведенных численных экспериментов предложена математическая модель лазерного нагрева жидкой среды в окрестности торца оптоволокна с последующим возникновением и развитием процесса кавитации, сопровождающимся формированием кумулятивной струи (рисунок 7). Объяснен механизм зарождения, роста и схлопывания парового пузырька с точки зрения процесса поверхностного массообмена на границе раздела жидкой и парообразной среды. Разработанный метод расчета динамики парового пузырька позволяет применять рассматриваемую модель кавитации для произвольного начального температурного распределения.

Численно исследован процесс термокавитации в окрестности торца оптоволокна, установленного в заполненную водой стеклянную трубку, погружённую в ограниченный объём, заполненный жидкостью. Установлено, что вытекающие и втекающие потоки разогретой жидкости в трубке, возникающие при росте и схлопывании парового пузырька, приводят к интенсивным горизонтальным потокам жидкости в зазоре между дном кюветы и нижним торцом трубки (рисунок 8). Показано, что в начальные моменты ускоренного роста и, особенно, в момент коллапса парового пузырька вблизи дна кюветы под нижним торцом трубки возникают мощные импульсы давления, способные эффективно влиять на поверхность дна кюветы, тогда как при схлопывании пузырька потоки жидкости устремлены в обратном направлении в трубку. Обнаруженные эффекты могут быть использованы для эффективной селективной очистки поверхности.

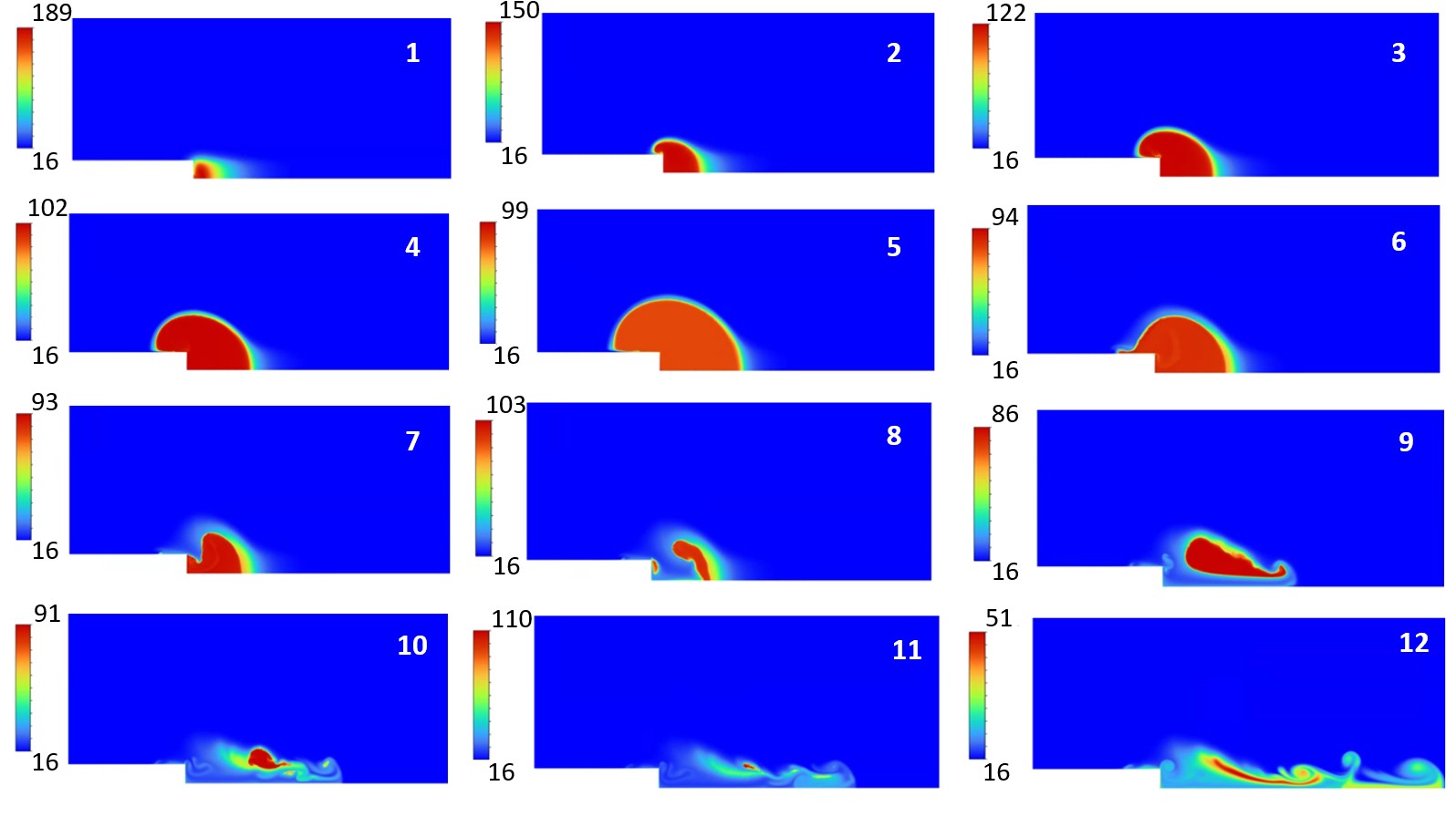
Рисунок 7 - Температурное поле в процессе роста и схлопывания парового пузырька и формирования кумулятивной струи.

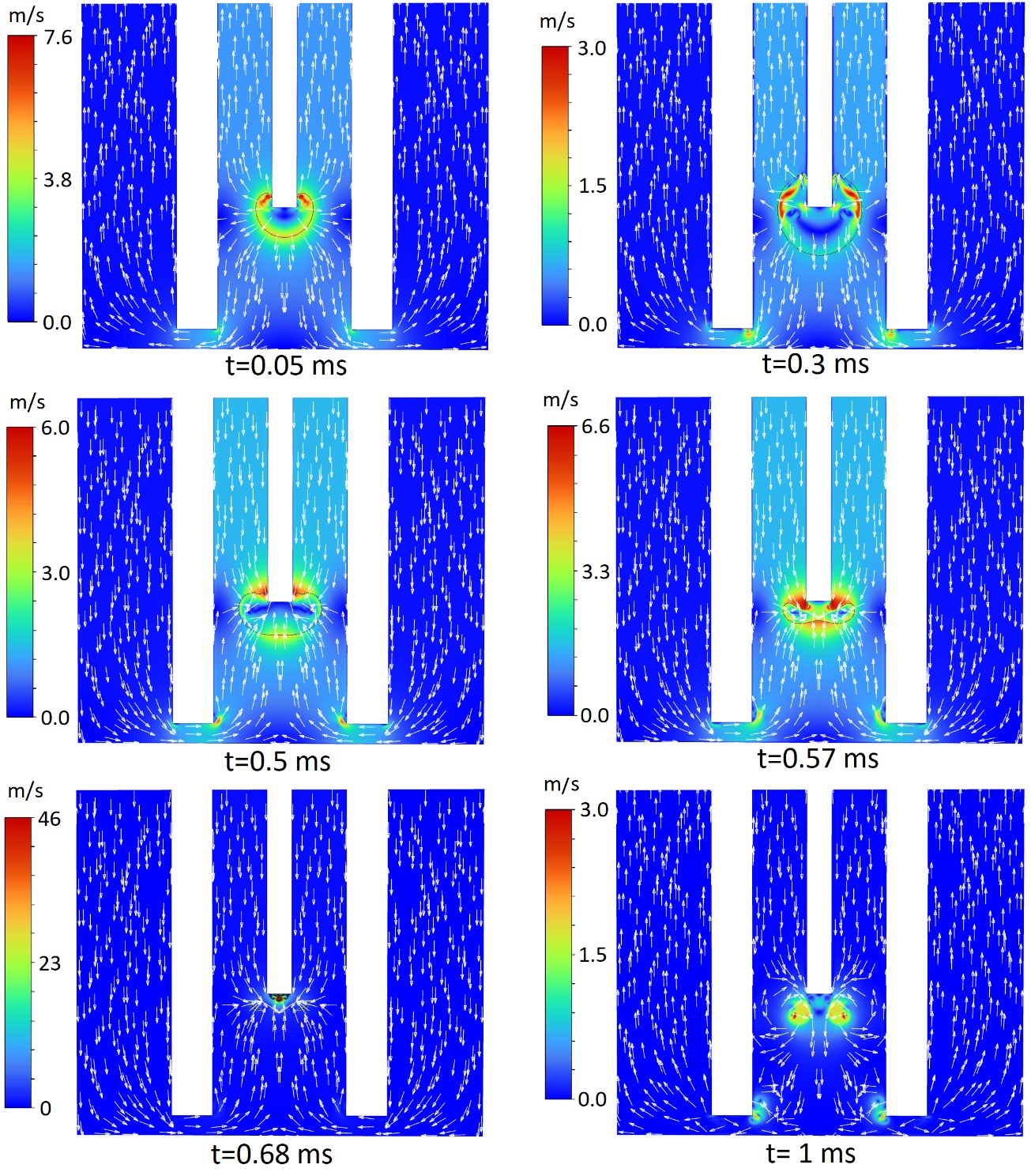
Рисунок 8 - Динамика потоков жидкости при схлопывании парового пузырька в заполненной водой стеклянной трубке

М.А. Гузев, Ю.В. Василевский, Е.П. Дац, И.А. Абушкин, Е.В. Хайдуков, В.М. Чудновский. Лазерная кавитация в трубке, погружённой в ограниченный объём, заполненный жидкостью. // Доклады Российской академии наук. Физика, технические науки. 2024. Т. 519. № 1. С. 19-25.

В.М Чудновский., М.А Гузев., Ю.В. Василевский, Е.П. Дац., А.В. Кулик. Особенности кавитации, инициированной на лазерном нагревательном элементе вблизи твердой плоской поверхности. // Письма в журнал технической физики. 2024. Т. 50, вып. 18. С. 3.

6. В рамках математической модели, основанной на нестационарном уравнении переноса излучения, предложены новые подходы к повышению точности восстановления коэффициента ослабления излучения в импульсной рентгеновской томографии рассеивающих сред, которые базируются на установлении функциональной зависимости реконструированных изображений от длительности зондирующих импульсов и проведением экстраполяционной процедуры. Методами математического моделирования установлено, что предложенные алгоритмы эффективно подавляют отрицательное влияние рассеянного излучения при восстановлении коэффициента ослабления и обладают высокой степенью устойчивости даже для сред, содержащих оптически плотные неоднородности при значительном уровне шума в проекционных данных.

Рисунок 9 - На рисунке (а) изображено внутреннее строение тестового фантома. На рисунках (b), (c) приведены результаты реконструкции коэффициента ослабления излучения при облучении импульсами длительностью порядка 100-200 пикосекунд по необработанным проекционным данным (b) и с использованием экстраполяционной процедуры (c).

Yarovenko I.P., Prokhorov I.V. An extrapolation method for improving the quality of tomographic images using multiple short-pulse irradiations //Journal of Inverse and Ill-posed Problems. 2024. V. 32. № 1. P. 57–74.

Yarovenko I.P., Vornovskikh P.A., Prokhorov I.V. Extrapolation of Tomographic Images Based on Data of Multiple Pulsed Probing // Journal of Applied and Industrial Mathematics. 2024. V. 18. № 3. P. 583–597.

7. Рассмотрены две системы массового обслуживания (МО), представимые дискретными марковскими процессами с заданными графами переходных интенсивностей. Первая модель построена объединением графов переходных интенсивностей систем или сетей МО и введением взвешенных ребер (переходных интенсивностей) между ними так, чтобы ее стационарное распределение стало вероятностной смесью стационарных распределений объединяемых систем (см. пример на рисунке 10). В результате функционирование объединенной системы в определенные моменты времени меняется с одного режима на другой. Вторая модель построена введением взвешенных ребер (переходных интенсивностей) так, чтобы ее стационарное распределение было, как в физической статистике, равномерным (см. пример на рисунке 11). По аналогии с потоком в детерминированной транспортной сети выделены состояния, в которых сумма входных интенсивностей не равна сумме выходных интенсивностей, и введены взвешенные ребра (переходные интенсивности), преобразующие эти неравенства в равенства. Такое преобразование может моделировать передачу информации от кратковременной памяти в долговременную.

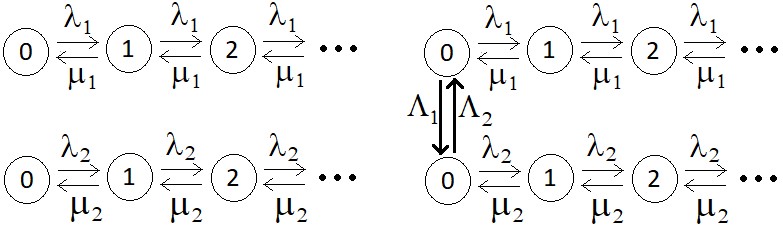
Рисунок 10 - Графы переходных интенсивностей одноканальных системы с бесконечным числом мест в очереди (слева) и объединенной первой модели (справа)

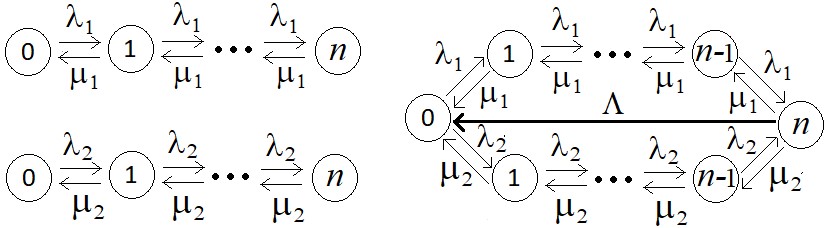
Рисунок 11 - Графы переходных интенсивностей одноканальной системы с числом мест в очереди равным n (слева) и объединенной второй модели (справа)

Tsitsiashvili G.Sh. Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modeling// Computation. 2024, 12, 195. DOI: 10.3390/computation12100195.

Цициашвили Г.Ш., Харченко Ю.Н. Управляемые системы массового обслуживания со стационарным равномерным распределением// Вестник ТГУ. Управление, вычислительная техника и информатика. 2024. Т. 68. С. 59-65. DOI: 10.17223/19988605/68/6.